miércoles, 11 de septiembre de 2013
sábado, 7 de septiembre de 2013
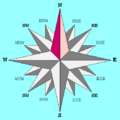
Rosa de los vientos
Una rosa de los vientos es un círculo que tiene marcados alrededor los rumbos en que se divide la horizonte. Su invención se atribuye a Raimundo Lulio, aunque la descripción pormenorizada que da Plinio el viejo en libro II,1 podría haber sido su referencia básica.circunferencia del
En las cartas de navegación se representa por 32 rombos (deformados) unidos por un extremo mientras el otro señala el rumbo sobre el círculo del horizonte. Sobre el mismo se sitúa la flor de lis con la que suelen representar el Norte que se documenta a partir del siglo XV.
También puede ser un diagrama que representa la intensidad media del viento en diferentes sectores en los que divide el círculo del horizonte.
Los nombres de los vientos
Estos nombres indican la procedencia del viento en España. En otros países hispanohablantes, los nombres son diferentes.
- SO - Sudoeste -- Lebeccio
- O - Oeste -- Poniente
- NO - Noroeste -- Mistral
- N - Norte -- Tramontana
- NE - Nordeste -- Gregario
- E - Este -- Levante
- SE - Sudeste -- Siroco
- S - Sur -- Mediodía
Los puntos cardinales
Los cuatro puntos cardinales son:
Para identificar mejor estos puntos, se puede usar nuestro cuerpo como referencia. Orientando nuestro frente hacia el Norte,estaría hacia atrás el Sur, a la derecha estaría el Este y la izquierda el Oeste.
Los cuatro rumbos laterales
- NE(Norte-Este)-Noreste
- SE(Sur-Este)-Sureste
- SO(Sur-Oeste)-Suroeste
- NO(Norte-Oeste)-Noroeste
Los ocho rumbos colaterales
- NNE (Nornordeste)
- ENE (Estenordeste)
- ESE (Estesudeste)
- SSE (Sudsudeste)
- SSO (Sudsudoeste)
- OSO (Oestesudoeste)
- ONO (Oestenoroeste)
- NNO (Nornoroeste)
Los dieciséis rumbos co-colaterales
Los rumbos co-colaterales toman su nombre de los rumbos laterales, agregándoseles "por" (en inglés "by") para indicar su relación con el rumbo lateral del cual toman su nombre. En la lista a continuación, se colocan los rumbos colaterales en donde no sea claro entre cuales rumbos van.
- NpE (Norte+Norte+Este+Norte)— Norte por el Este
(Nornoreste)
- NEpN (Norte-Norte-Este-Este)—Nordeste por el Norte
- NEpE (Este-Norte-Este+Norte)— Nordeste por el Este
(Estenoreste)
- EpN (Este-Norte-Este-Este)— Este por el Norte
- EpS (Este-Sur-Este-Este)— Este por el Sur
(Estesureste)
- SEpE (Este-Sur-Este-Sur)— Sudeste por el Este
- SEpS (Sur-Sur-Este-Este)— Sudeste por el Sur
(Sursureste)
- SpE (Sur-Sur-Este-Sur)— Sur por el Este
- SpO (Sur-Sur-Oeste-Sur)— Sur por el Oeste
(Sursuroeste)
- SOpS (Sur-Sur-Oeste-Oeste)— Sudoeste por el Sur
- SOpO (Oeste-Sur-Oeste-Sur)— Sudoeste por el Oeste
(Oestesuroeste)
- OpS (Oeste-Sur-Oeste-Oeste)— Oeste por el Sur
- OpN (Oeste-Norte-Oeste-Oeste)— Oeste por el Norte
(Oestenoroeste)....
- NOpO (Oeste-Norte-Oeste-Norte)— Noroeste por el Oeste
- NOpN (Norte-Norte-Oeste-Oeste)— Noroeste por el Norte
(Nornoroeste)
- NpO (Norte-Norte-Oeste-Norte)— Norte por el Oeste
El rumbo
La determinación de un rumbo empleando los puntos cardinales o el ángulo respecto al norte, indicando un ángulo en grados sexegesimal de cero a 180 este, o de cero a 180 oeste, siendo el ángulo de cero grado la dirección norte.
También puede indicarse el rumbo en grados sexagesimales de cero a 360 grados, en sentido horario, hacia el este.
La indicación del rumbo en milesimas, dividiendo la circunferencia en 6400 partes iguales, midiéndolas en sentido horario desde el norte.
La división de la circunferencia en 6400 milésimas da lugar a que todos los puntos cardinales son un múltiplo exacto de esta unidad angular, ver la figura.
Sectores (en grados sexagesimales) correspondientes a cada viento
- Viento del norte o tramuntana (N): de 337.5° a 22.5°
- Viento del noreste o gregal (NE): de 22.5° a 67.5°
- Viento del este o levante (E): de 67.5° a 112.5°
- Viento del sureste o xaloc (SE): de 112.5° a 157.5°
- Viento del sur o migjorn (S): de 157.5° a 202.5°
- Viento del suroeste, llebeig o garbí (SW): de 202.5° a 247.5°
- Viento del oeste o poniente (W): de 247.5° a 292.5°
- Viento del noroeste o mistral (NW): de 292.5° a 337.5°
Uso de la rosa de los vientos en el diseño de los aeropuerto
Se realiza un análisis de vientos con datos estadísticos de intensidad y dirección del viento en el lugar del emplazamiento, medidos durante un periodo de tiempo de al menos 5 años y como mínimo 8 veces diarias con intervalos iguales.Si no es posible realizar las mediciones en el propio emplazamiento, se podrán utilizar estadísticas de lugares cercanos donde haya un observatorio, teniendo en cuenta que puede haber diferencias entre las condiciones del entorno respectivas.
Estas observaciones se agrupan en intervalos de intensidad de velocidad, medida en nudos, y para las direcciones se divide cada cuadrante (N, S, W, E) en 4 sectores, de modo que se tienen 16 sectores de dirección de viento (nº de observaciones y frecuencias).
La representación gráfica de estos datos de intensidad y dirección de vientos se confecciona llevándolos a un diagrama de círculos concéntricos, cuyos radios son a escala las frecuencias de las observaciones en en cada sentido. Este diagrama es conocido como rosa de vientos.2
Galería
Simetría Axial
La simetría axial (también llamada rotacional o radial o cilíndrica) es la simetría alrededor de un eje, de modo que un sistema tiene simetría axial o axisimetría cuando todos los semiplanos tomados a partir de cierta mediatriz y conteniéndolo presentan idénticas características.También puede decirse que es una isometría indirecta e involutiva
Dada una recta e se llama simetría axial de eje e al movimiento que transforma a un punto P en otro punto P' verificando que:
- El segmento PP' es perpendicular a
. - Los puntos P y P' equidistan del eje .
Dicho de otra forma el eje es la mediatriz del segmento PP'
es la mediatriz del segmento PP'
La simetría axial no solo se presenta entre un objeto y su reflexión, pues muchas figuras que mediante una línea pueden partirse en dos secciones que son simétricas con respecto a la línea. Estos objetos tienen uno (o más) ejes de simetría.
La simetría axial se da cuando los puntos de una figura coinciden con los puntos de otra, al tomar como referencia una línea que se conoce con el nombre de eje de simetría. En la simetría axial se da el mismo fenómeno que en una imagen reflejada en el espejo.
A los puntos que pertenecen a la figura simétrica se les llama puntos homólogos, es decir, A’ es homólogo de A, B’ es homólogo de B, y C’ es homólogo de C. Además, las distancias existentes entre los puntos de la figura original son iguales que las distancias entre los puntos de la figura simétrica. En este caso: La simetría axial se puede dar también en un objeto con respecto de uno o más ejes de simetría.
Si se doblara la figura sobre el eje de simetría trazado, se podría observar con toda claridad que los puntos de las partes opuestas coinciden, es decir, ambas partes son congruentes.
Física
Un cierto número de problemas físicos de interés, especialmente relacionados con la teoría de campos, los medios continuos o la teoria cuantica son más fáciles de resolver cuando los datos de partida tiene simetría axial, ya que la solución para ciertas magnitudes incógnitas también tendrá simetría axial. Eso permite reducir un problema con tres coordenadas espaciales a un problema de dos variables. Por ejemplo en varias áreas de la resolución de ciertos problemas requiere estudiar la ecuación de Poisson siguiente:
Cuando la función "fuente" tiene simetría axial, es decir:
trazado de curvas
Para trazar unas
curvas se necesitan muchas cosas como: dominio, intervalo, simetría. Límites,
continuidad, asíntotas derivadas, tangentes, valores extremos,
intervalos de incremento y decremento, concavidad y puntos de inflexión; todo
esto nos revela las características importantes de las funciones.
La aplicación del cálculo permite descubrir los
aspectos más interesantes de las gráficas y, en muchos casos, calcular
exactamente los puntos máximos y mínimos y los puntos de inflexión, y no solo
en forma aproximada.
TRAZADO DE CURVAS TÉCNICAS
En esta unidad Trazaremos curvas técnicas (óvalos,
ovoides y espirales),
estos estas formados por arcos de
circunferencia tangentes.
1- Ovalo: Curva
cerrada y plana, compuesta por arcos de circunferencia tangentes entre sí.
Tiene dos ejes de simetría perpendicular entre sí, y que se cortan en sus
puntos medios.
Para trazar un ovalo dado el eje Mayor
Primero trazamos una recta siendo el inicio el
punto A y el final el punto B el eje mayor.
Se divide en tres partes iguales, quedando las
divisiones de la siguiente manera: el punto de inicio A, los puntos de
intersección M y N y el punto final B.
Con centro en la intersección M y con radio en a A
se describen la primera circunferencia.
Con centro en la intersección N y con radio en a B
se describen la segunda circunferencia.
Debemos de trazar una diagonal que este entre el
centro de M y N hasta los puntos de encuentro donde se interceptan las
circunferencias siendo estos los puntos O y P.
Trazamos una diagonal desde O pasando por M y N
individualmente para obtener los puntos H y G.
Trazamos una diagonal desde P pasando por M y N
individualmente para obtener los puntos E y F.
Con centro en P y radio en E se describe el arco E
F.
Con centro en O y radio en G se describe el arco G
H.
Para trazar un ovalo
dado el eje menor
Primero trazamos una recta siendo el inicio el
punto A y el final el punto B el eje mayor.
Y una diagonal que pase por el centro de AB siendo
el punto medio O y así se describe el eje menor CD.
En el punto medio O de este eje y con radio igual a
la mitad del mismo se describe una circunferencia.
Los puntos donde la circunferencia corta al eje
mayor serán M y N.
Trazamos una diagonal desde C pasando por M y se
obtiene el Punto H.
Trazamos una diagonal desde C pasando por N y se
obtiene el Punto G.
Trazamos una diagonal desde D pasando por M y se
obtiene el Punto E.
Trazamos una diagonal desde D pasando por N y se
obtiene el Punto F.
Con centro en C y radio en D se describe un arco de
circunferencia GDH.
Con centro en D y radio en C se describe un arco de
circunferencia ECF.
Con centro en M y radio E se describe el arco EAH y
con centro en N y radio en F se describe el arco FBG, con lo que se obtiene el
ovalo buscado.
2- Ovoide: Curva
cerrada y plana, compuesta por arcos de circunferencias tangentes entres si,
dos arcos de igual radio y otros de radio distinto, siendo el mayor de ellos
una semicircunferencia. Tiene un solo eje de simetría, que contiene a los
centros de los arcos desiguales.
Para trazar un ovoide
dado el eje menor
Se halla el punto medio O1 del
eje conocido y con centro en él se traza una circunferencia que tenga como
diámetro el propio eje.
Se determina el punto O2 en la
intersección de la circunferencia con la mediatriz del eje AB.
Se trazan las rectas que pasan por los extremos A y
B del eje y el punto O2, antes hallado.
Con centro en A y en B se trazan dos arcos de radio
igual al diámetro hasta que corten a las prolongaciones de las rectas que pasan
por los puntos A y B y O2.
Haciendo centro en O2 y abriendo
hasta las intersecciones de los arcos antes descritos con las prolongaciones de
las rectas, trazamos el arco que completa el ovoide.
3- Espiral: Es
una curva plana, abierta, generado por un punto P, situada en origen O de una
semirrecta que se desplaza sobre ella con un movimiento longitudinal, al mismo
tiempo que la semirrecta gira alrededor de O con un movimiento circular.
Para trazar un espiral de
dos centros y paso constante
Se determina la magnitud 2A del paso constante y se
halla su punto medio 1.
Con centro en el punto 1 se traza una
semicircunferencia de diámetro 2A.
Se continua la espiral trazando el arco AC, con
centro en el punto 2 y radio 2A.
Se describe después el arco CD, volviendo al punto
1 como centro y abriendo el compas hasta el punto donde termino el último arco
trazado.
jueves, 5 de septiembre de 2013
SIMETRIA CENTRAL
SIMETRIA CENTRAL
Una simetría central, de centro el punto O, es un movimiento del plano con el que a cada punto P del plano le hace corresponder otro punto P', siendo O el punto medio del segmento de extremos P y P'.
Coordenadas mediante una simetría de centro O(0,0)
P' = (-x, -y)
x' = -x y' = -y
Coordenadas mediante una simetría de centro O(a, b)
Composición de simetrías centrales
Con el mismo centro
Con distinto centro
Isometrico 01
.gif)
ISOMETRIA
En diseño industrial se representa una pieza desde diferentes puntos de vista, perpendicular a los ejes coordenados naturales. Una pieza con movimiento mecánico presenta en general formas con ejes de simetría o caras planas. Tales ejes, o las aristas de las caras, permiten definir una proyección ortogonal.En el diseño y el dibujo técnico
Se puede fácilmente dibujar una perspectiva isométrica de la pieza a partir de tales vistas, lo que permite mejorar la comprensión de la forma del objeto.
En arquitectura
La perspectiva de este dibujo del castillo no es isométrica, si así lo fuera, las torres del castillo estarían dibujadas con la misma altura y diámetro, además las líneas de cumbreras de los tejados serían paralelas entre si, formando un rombo o romboide dependiendo de la planta del castillo. este sistema en muchos dibujos de sus edificios, evitando acentuar la importancia de unos volúmenes sobre otros e independizándose del punto de vista del observador.
.jpg)
En videojuegos
Cierto número de videosjuegos pone en acción a sus personajes utilizando un punto de vista en perspectiva isométrica, o mejor dicho, en la jerga usual, en "perspectiva 3/4". Desde un ángulo práctico, ello permite desplazar los elementos gráficos sin modificar el tamaño, limitación inevitable para ordenadores con baja capacidad gráfica.
A fin de evitar el pixelado, en algunos casos se llevó la proyección a un sistema 2:1, vale decir a una inclinación de 26,6º (arctan 0,5) en lugar de 30º, que no corresponde a una proyección isométrica propiamente dicha, sino "dimétrica".
El progresivo incremento en las capacidades gráficas de los ordenadores ha posibilitado el uso cada vez más generalizado de sistemas de proyección más realistas, basados en la perspectiva naturalmente percibida por el ojo humano: la perspertiva conica
Suscribirse a:
Entradas (Atom)